【题解】 [NOI2009]诗人小G 四边形不等式/决策单调性优化DP luoguP1912 | Qiuly's blog!

【题解】 [NOI2009]诗人小G 四边形不等式/决策单调性优化DP luoguP1912

Posted on | Edited on | In | Comments:

神奇的题目 $QvQ$ ，卡了我好久。

哎，主要是细节要处理到位，否则就会 WA 声满片。

记录一下我壮观的提交记录：

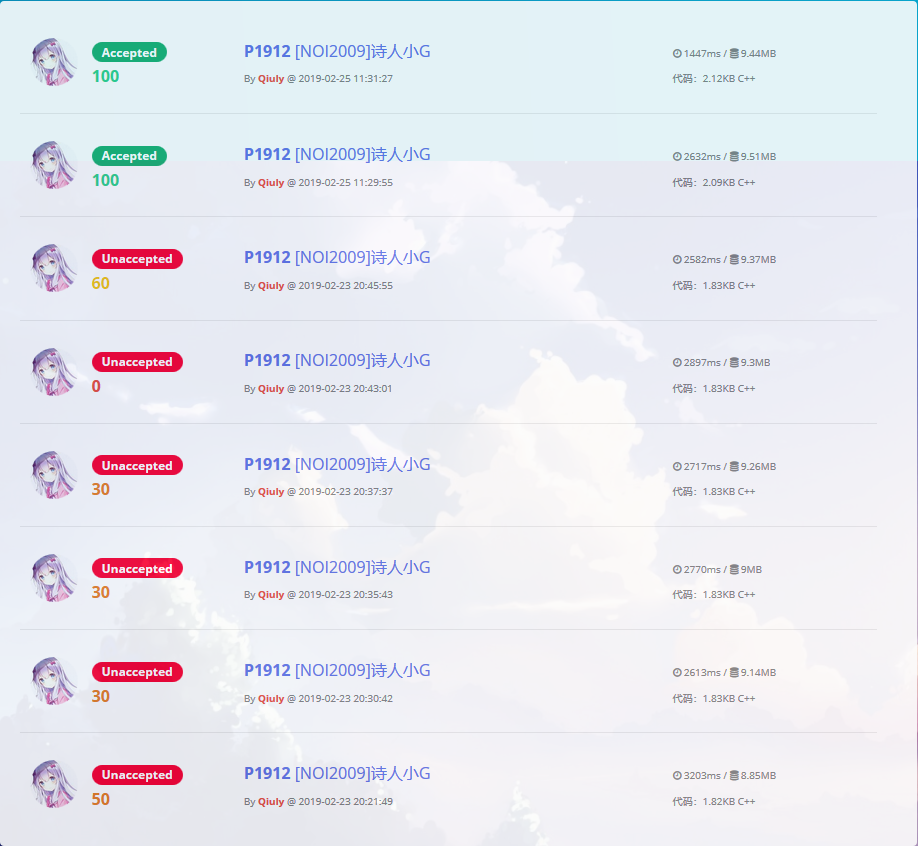
太杯具了 $QvQ$

(扯谈扯不下去了…….)

进入正题吧。

路人甲：$bzoj$ 上居然没有这道题？
导演：赶紧走开，不管你的事

这题明显是 $DP$，我们可以很简单的得到 $DP$ 方程：

设 $f[i]$ 表示对前 $i$ 句诗排版后的最小不协调度，那么很显然，对于一个现在我们需要转移的 $i$，我们会找到一个最优的 $j$ ，使得第 $j+1$ 句到第 $i$ 句组成一个新的行。那么之前的行的总共的最小不协调度显然是 $f[j]$，现在我们就来计算一下 $f[i]$ 的最小不协调度。

显然，是下式(其中 $sum$ 是句子长度的前缀和)：

这就是状态转移方程，的确很好理解。但是……这样子做是 $O(N^2)$ 的复杂度，只能拿 $30$ 分。

而按照题目的数据范围，正解的复杂度因该是 $O(n log n)$ 左右。接下来考虑怎么优化。

经打表观察发现，如果我们将每次用作转移 $i$ 的最优的 $j$ 存起来，输出时会发现，$j$ 是单调递增的。

证明的话的确不好证，可以看看 $lyd$ 的书。但是按照实际理解一下是可以的，我们将 $j$ 后面的一直到 $i$ 的句子组成了新的一行，那么如果 $j$ 不单调上升的话，新的一句将会变的很长很长很长，那么这时这句造成的不协调度将会以几何数的形式疯狂增长，那么唯一的方法就是将这句长句断句，这样子 $j$ 就会变大，可以感性理解一下 $QvQ$。

但是我们知道了 $j$ 是单调上升的这条性质有什么用呢？

很显然，每一次转移的时候不必往前找了，直接往后找。

我们维护一个队列，队列里的每一个元素有三个变量：$l,r,c$ ，其中 $l$ 和 $r$ 表示 $c$ 这个决策的适用范围，并且在这个范围中 $c$ 是最优的 $j$。

那么现在有了一个新的 $i$，考虑怎么维护这个队列。

我们可以先找到 $i$ 所在的范围的最优的 $j$，那么这时我们检查队头，如果队头的范围已经不包括 $i$ 了，那么直接弹出，因为既然队头的范围不包括 $i$ 了，那么这个队头对 $i+1$ 及后面的元素都不能产生贡献，故直接弹出。

弹出无用的队头后，转移的话就是 $O(1)$ 了：直接取队头转移不就好了吗？

那么现在考虑怎么将 $i$ 加入这个队列，或许这个 $i$ 也会对后面的元素产生贡献。

我们检查当前的队尾，怎么判断这个队尾是否比 $i$ 更优呢？现在队尾的范围是 $l,r$ ，如果 $i$ 更新 $l$ 比 $c$ 更新 $l$ 更优，显然 $i$ 会比当前 $l,r$ 范围类的所有的 $c$ 更优，故弹出队尾。

那么，假设现在我们碰到了一个队尾，其中 $i$ 更新 $r$ 更优， $c$ 更新 $l$ 更优，怎么办呢？也就是说这个元素的范围中分成两半，前一半 $c$ 更新更优，后一半 $i$ 更新更优，显然要拆成两个队列元素。那么我们怎么知道这个位置呢？二分！

那么这个时候我们可以得到答案了，只是输出怎么办呢？

很简单，每次转移的时候记录一下转移自哪里，这就是分行，然后输出即可。

最后就是精度问题。

题目要求，如果 $f[n]$ (即所有句子排版后的最小不协调度) 还是大于了 $1e18$ ，那么输出 “$Too \ hard\ to\ arrange$”，但是如果在 $DP$ 的过程中就炸了 $long \ long$，那就 $GG$ 了。所以我们使用 $long \ double$ ，精度更高，(不会 $int$ 的，这辈子也不会用 $int$ 的)。

Code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
#include<cmath>
#include<cstdio>
#include<string>
#include<cstring>
#include<iostream>
#include<algorithm>

typedef long long ll;
typedef long double ld;

const int NS=1e5+2;
const int inf=1e9+9;

int T,N,L,P;
int head,tail;
int last[NS],ans[NS],Next[NS];
struct Node{int c,l,r;}q[NS];
char s[NS][35];
ld sum[NS],f[NS];

template <typename _Tp> inline void IN(_Tp&x){
    char ch;bool flag=0;x=0;
    while(ch=getchar(),!isdigit(ch))if(ch=='-')flag=1;
    while(isdigit(ch))x=x*10+ch-'0',ch=getchar();
    if(flag)x=-x;
}

void clear(){
    memset(last,0,sizeof(last));
    memset(sum,0,sizeof(sum));
    memset(q,0,sizeof(q));
    memset(s,0,sizeof(s));
    memset(f,0,sizeof(f));
}

ld pows(ld x,int y){//快速幂
    ld ans=1;
    for(;y;y>>=1,x*=x)if(y&1)ans*=x;
    return ans;
}

ld val(int j,int i){//转移函数
    return f[j]+pows(abs(sum[i]-sum[j]-L-1),P);
}

void half(int i){//二分过程
    int now=q[tail].c,ls=q[tail].l,rs=q[tail].r;//当前队尾范围
    int ret=q[tail].r+1;
    while(ls<=rs){
        int mid=(ls+rs)>>1;
        if(val(i,mid)<=val(now,mid))rs=mid-1,ret=mid;//i更优
        else ls=mid+1;//c更优
    }
    if(ret!=q[tail].l)q[tail].r=ret-1;//分成了两半
    else --tail;//整个元素都比不过i
    if(ret<=N)q[++tail]=(Node){i,ret,N};//i分了一个区间时，加入新元素
}

void output(){//值得拥有的鬼畜输出
    if(f[N]>1e18)puts("Too hard to arrange");//无解，放心判1e18
    else{
        printf("%lld\n",(ll)(f[N]+0.5));//注意精度问题
        for(int i=N;i;i=last[i])Next[last[i]]=i;//输出
        int now=0;
        for(int i=1;i<=N;++i){
            now=Next[now];
            for(int j=i;j<now;++j)printf("%s ",s[j]);
            printf("%s\n",s[now]);
            i=now;
        }
    }
    puts("--------------------");//注意
    return;
}

int main(){
    IN(T);
    while(T--){
        clear();
        IN(N),IN(L),IN(P);
        for(int i=1;i<=N;++i){
            scanf("%s",s[i]);
            sum[i]=sum[i-1]+strlen(s[i])+1;//做前缀和
            /*因为输出是有空格的，所以加上一个1*/
        }
        q[head=tail=1]=(Node){0,1,N};//初始元素
        for(int i=1;i<=N;++i){
            while(head<tail&&q[head].r<i)++head;//淘汰无用队头
            ++q[head].l;
            f[i]=val(q[head].c,i);//O(1) 转移
            last[i]=q[head].c;//记录“转移自哪里”
            while(head<tail&&val(i,q[tail].l)<=val(q[tail].c,q[tail].l))tail--;//弹出劣质队尾
            half(i);//二分
        }
        output();//鬼畜输出
    }		
    return 0;//终于结束
}

最后，我有个问题。

这是写的什么文章啊 $QvQ$ ，让我们来猜测一下。


白日依山尽，黄河入海流，欲穷千里目，更上一层楼。

这是 小 $G$ 写的？作者明明不是小 $G$ 好不好。

$QvQ$ 有毒啊……

本文标题:【题解】 [NOI2009]诗人小G 四边形不等式/决策单调性优化DP luoguP1912

文章作者:Qiuly

发布时间:2019年02月25日 - 00:00

最后更新:2019年03月29日 - 13:52

原始链接:http://qiulyblog.github.io/2019/02/25/[题解]luoguP1912/

许可协议: 署名-非商业性使用-禁止演绎 4.0 国际 转载请保留原文链接及作者。